The Cell Growth Model
Theory
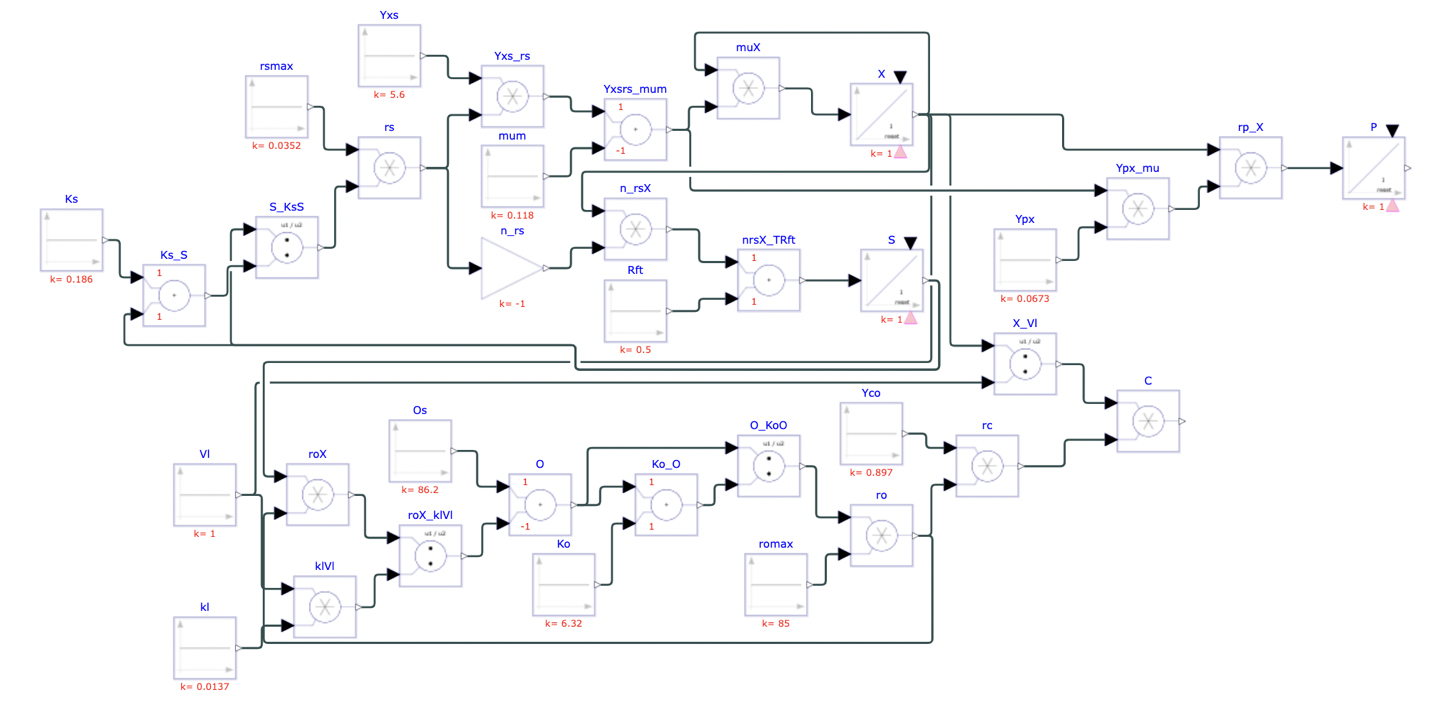
Cell growth can be modeled in countless different ways, depending on specific conditions, processes, and experimental designs. This model is based on an experiment done by Axel Munack and Clemens Posten[^1], measuring cell growth via fermentation in an isolated culture. The model takes into consideration cell metabolism, limiting rates, energy balance, and reaction equations of the system. The first step of modelling growth requires simplifying the metabolic structure of a cell into only the most important pathways–this includes hydrolysis of sucrose into glucose and fructose by extracellular enzymes, uptake of glucose and fructose into the cell, and glycolysis of carbohydrates into smaller components, which, along with oxygen, are used for cell energy. Cell metabolism processes form a product which is excreted from the cell. Carbon dioxide is a byproduct of energy production, and most of it is also excreted from the cell. The latter three components of the model build off this simplified structure and are represented by three categories of equations.
Equations
Limiting Rates
For simplicity, glucose and fructose are considered one substrate, S. The substrate uptake rate is given by
$$r_{S} = r_{S,max} \bullet \frac{S}{k_{s} + S}$$
Similarly, the oxygen uptake rate is given by
$$r_{O} = r_{O,max} \bullet \frac{O}{k_{O} + O}$$
Carbon dioxide production is assumed to be proportional to oxygen consumption and is given by
$$r_{C} = y_{C,O} \bullet r_{O}$$
The formation of the product is proportional to growth and is given by
$$r_{P} = y_{P,X} \bullet \mu$$
Energy Balance
The oxidation of substrate forms the high-energy bonds in ATP molecules, which are used as cell energy. A large amount of energy is used to synthesize new cell material for growth, while another portion is allotted to active transport and structural processes. A small amount is used for maintenance, independent of growth. If oxygen uptake is the growth determining factor, the growth rate is represented by:
$$\mu = y_{X,O} \bullet r_{O} - \mu_{m}$$
If substrate uptake is the determining factor, the growth rate is instead:
$$\mu = y_{X,S} \bullet r_{S} - \mu_{m}$$
Since the model assumes substrate concentration is limited, the latter equation is used as the growth rate.
Reactor Equations
The rates of change in cell concentration, substrate concentration, and product concentration are described by:
$$\frac{dX}{dt} = \mu \bullet X$$
$$\frac{dS}{dt} = - r_{S} \bullet X + R_{f}(t)$$
$$\frac{dP}{dt} = r_{P} \bullet X$$
respectively.
Dissolved oxygen and carbon dioxide concentration are modelled by the following algebraic equations:
$$r_{0} \bullet X = (O_{s} - O) \bullet k_{L} \bullet V_{L}$$
$$C = r_{C} \bullet \frac{X}{V_{L}}$$
Parameters
The state functions, intermediate equations, and parameters are defined as follows:
| States | Definition | Initial Value |
|---|---|---|
| X | cell concentration | $$4\ g \bullet l^{- 1}$$ |
| O | dissolved oxygen concentration | $$0.022\ %$$ |
| P | product concentration | $$5$$ |
| S | substrate concentration | $$50\ g \bullet l^{- 1}$$ |
| C | carbon dioxide concentration | $$1.059\ %$$ |
| Intermediates | Definition |
|---|---|
| $$\mathbf{r}_{\mathbf{S}}$$ | substrate uptake rate |
| $$\mathbf{r}_{\mathbf{O}}$$ | oxygen uptake rate |
| $$\mathbf{r}_{\mathbf{C}}$$ | carbon dioxide production rate |
| $$\mathbf{r}_{\mathbf{P}}$$ | product formation rate |
| $$\mathbf{\mu}$$ | cell growth rate |
| Parameters | Definition | Experimental Value |
|---|---|---|
| $$\mathbf{r}_{\mathbf{S,max}}$$ | maximum substrate uptake rate | $$0.01519\ % \bullet g^{- 1} \bullet d^{- 1}$$ |
| $$\mathbf{r}_{\mathbf{O,max}}$$ | maximum oxygen uptake rate | $$85.0\ % \bullet g^{- 1} \bullet d^{- 1}$$ |
| $$\mathbf{\mu}_{\mathbf{m}}$$ | diminution of growth by maintenance | $$0.118{\ d}^{- 1}$$ |
| $$\mathbf{y}_{\mathbf{C,O}}$$ | carbon dioxide production constant | $$0.897$$ |
| $$\mathbf{y}_{\mathbf{P,X}}$$ | product formation constant | $$0.0673\ g^{- 1}$$ |
| $$\mathbf{y}_{\mathbf{X,S}}$$ | substrate consumption constant | $$5.60\ g \bullet %^{- 1}$$ |
| $$\mathbf{k}_{\mathbf{s}}$$ | substrate concentration when growth is half of max. growth rate | $$0.186\ %$$ |
| $$\mathbf{k}_{\mathbf{O}}$$ | oxygen concentration when growth is half of max. growth rate | $$6.32\ %$$ |
| $$\mathbf{O}_{\mathbf{s}}$$ | total oxygen concentration | $$86.2\ %$$ |
| $$\mathbf{k}_{\mathbf{L}}$$ | oxygen dissolution constant | $$0.0137\ h \bullet l^{- 1} \bullet d^{- 1}$$ |
| $$\mathbf{V}_{\mathbf{L}}$$ | aeration rate | $$1$$ |
| $$\mathbf{R}_{\mathbf{f}}\mathbf{(t)}$$ | feed of substrate during cultivation | $$0.05$$ |
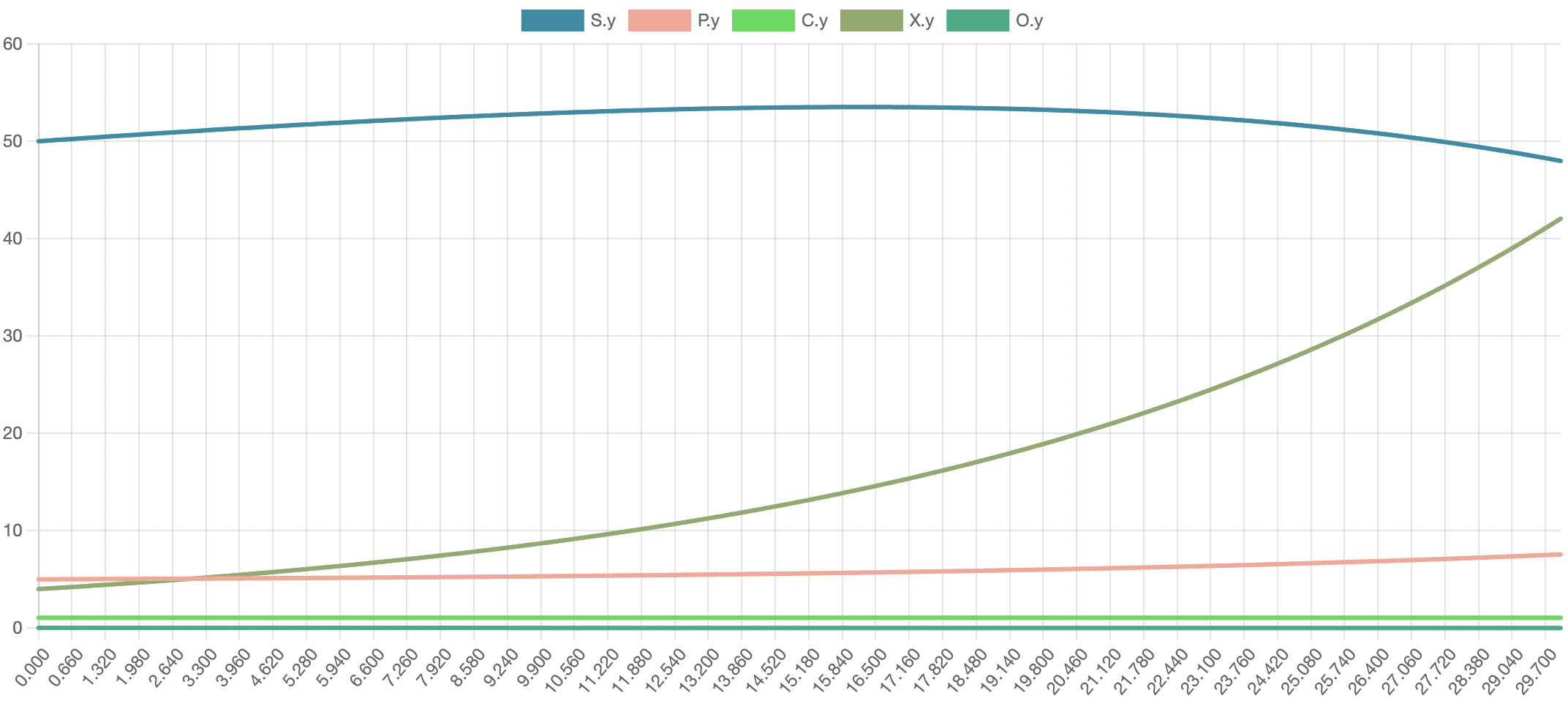
Munack and Posten’s experiment was modeled in Physhub using the above equations and experimentally derived values. The simulation was run for 30 units of time, roughly corresponding to the 30 days over which the original experiment was conducted.
Results
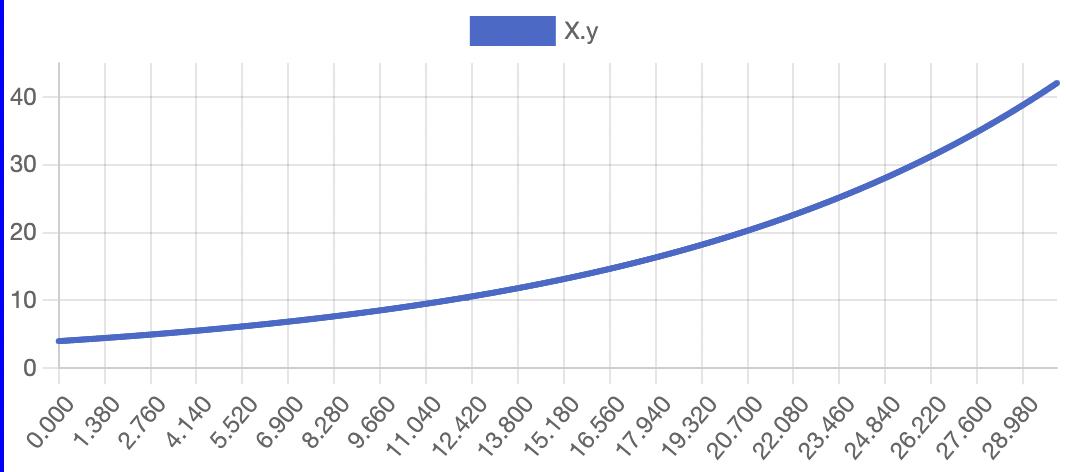
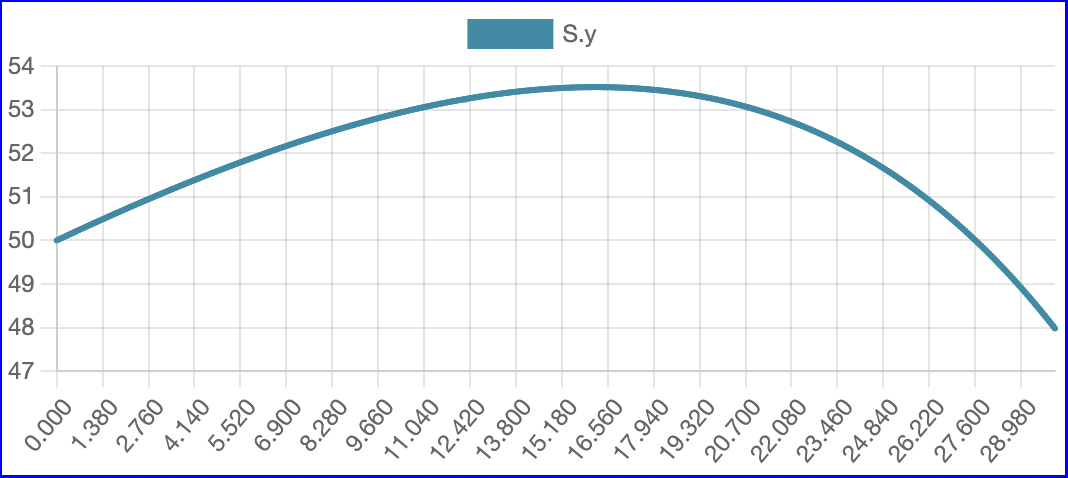
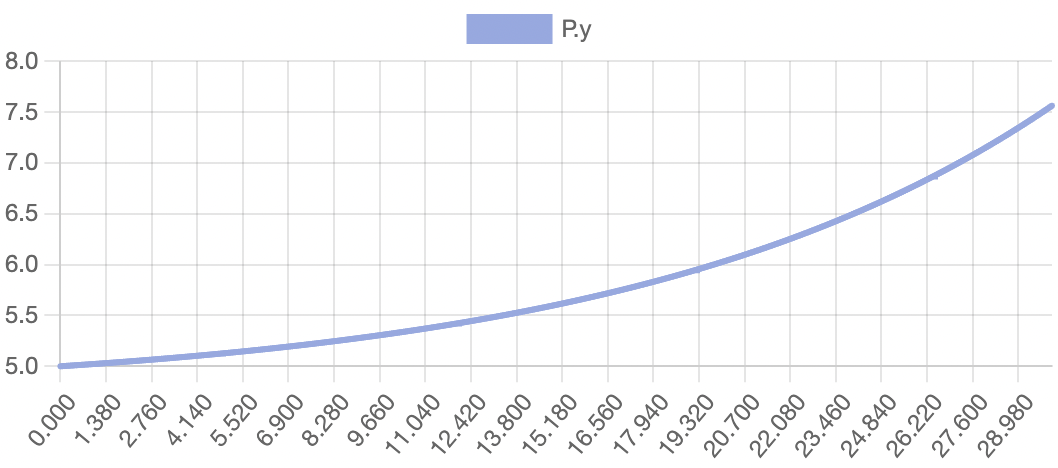
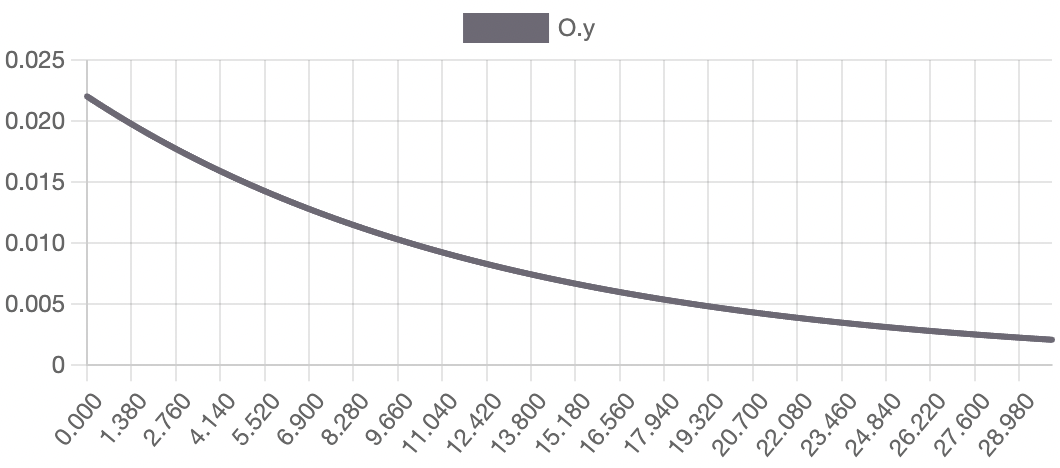
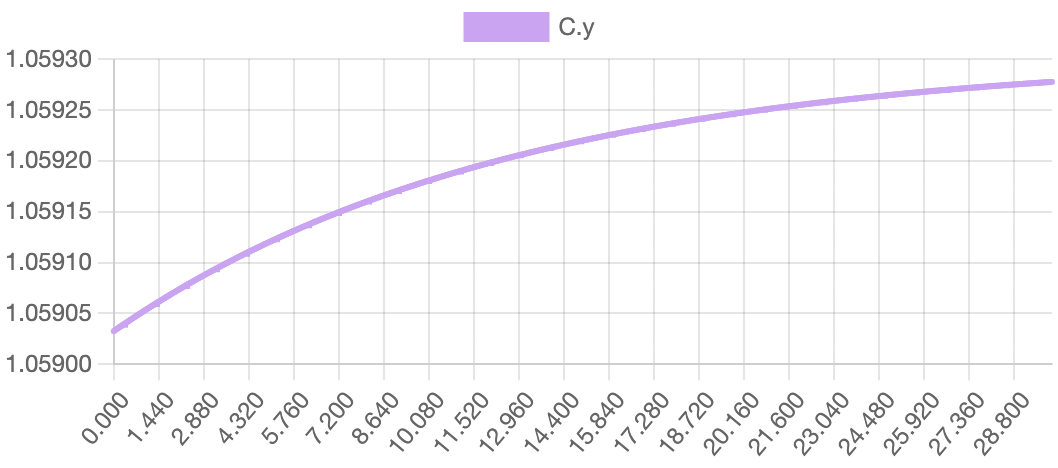
The model successfully visualizes the dynamics of cell growth in an isolated culture and is sufficiently accurate to the experimental data outlined in the original report. As predicted, cell concentration, product concentration, and carbon dioxide concentration increased over the simulation time while substrate concentration and dissolved oxygen concentration decreased. Although this model can represent cell growth dynamics, it is derived from Munack and Posten’s research and thus highly specific to their methods and results. This model may be difficult to reuse with different parameter values, and it may better serve as a reference point for building other specific experimental models.
References
[^1]: Munack, Axel & Posten, Clemens. (1989). Design of Optimal Dynamical Experiments for Parameter Estimation. Proceedings of the American Control Conference ACC. 89. 2010 - 2016. 10.23919/ACC.1989.4790520.