A SIR Epidemic Model
The Theory
The SIR ((susceptible-infectious-recovered )) epidemic model is one of the most basic compartmental models for infectious diseases. In this model, individuals are born with no immunity ((susceptible)) and encounter the disease at some point, becoming infectious. Individuals who recover gain total immunity and are unable to contract the disease again. The rate of disease spread is determined by ß, the probability of transmitting disease between susceptible and infected individuals. The rate of recovery is given by γ, the inverse of the average duration of infection. Assuming a closed population and a non-fatal disease, all susceptible individuals will become infected and recover. This model can be applied to a variety of diseases, but it is most used for highly infectious diseases with lifelong immunity upon recovery, such as measles, rubella, and pertussis.
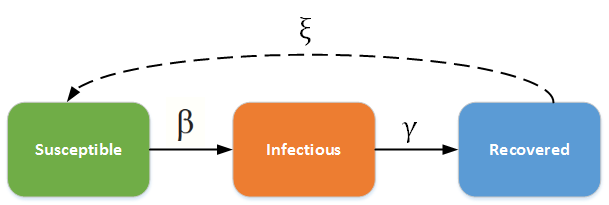
The Model
Equations
This model is represented by a set of three differential equations^1:
$$\frac{dS}{dt} = \frac{- ßSI}{N}$$
$$\frac{dI}{dt} = \frac{ßSI}{N} - \gamma I$$
$$\frac{dR}{dt} = \gamma I$$
where S = number of susceptible individuals, I = number of infected individuals, R = number of recovered individuals, ß = rate of infection ((constant)), γ = rate of recovery ((constant)), and N = S + I + R = total population ((constant)).
Parameters
The values of the constants ß and N are chosen based on the disease and population of interest. Since ß is a probability value, it ranges from 0 to 1. Greater ß value corresponds to higher infectiousness. N is usually selected as the total population value, but in certain cases, it may be simpler to choose N to be 1. This allows the model to directly deal with proportions of the population instead of large numbers. γ is calculated by taking the inverse of the average duration of infection, and thus it is typically a smaller decimal.
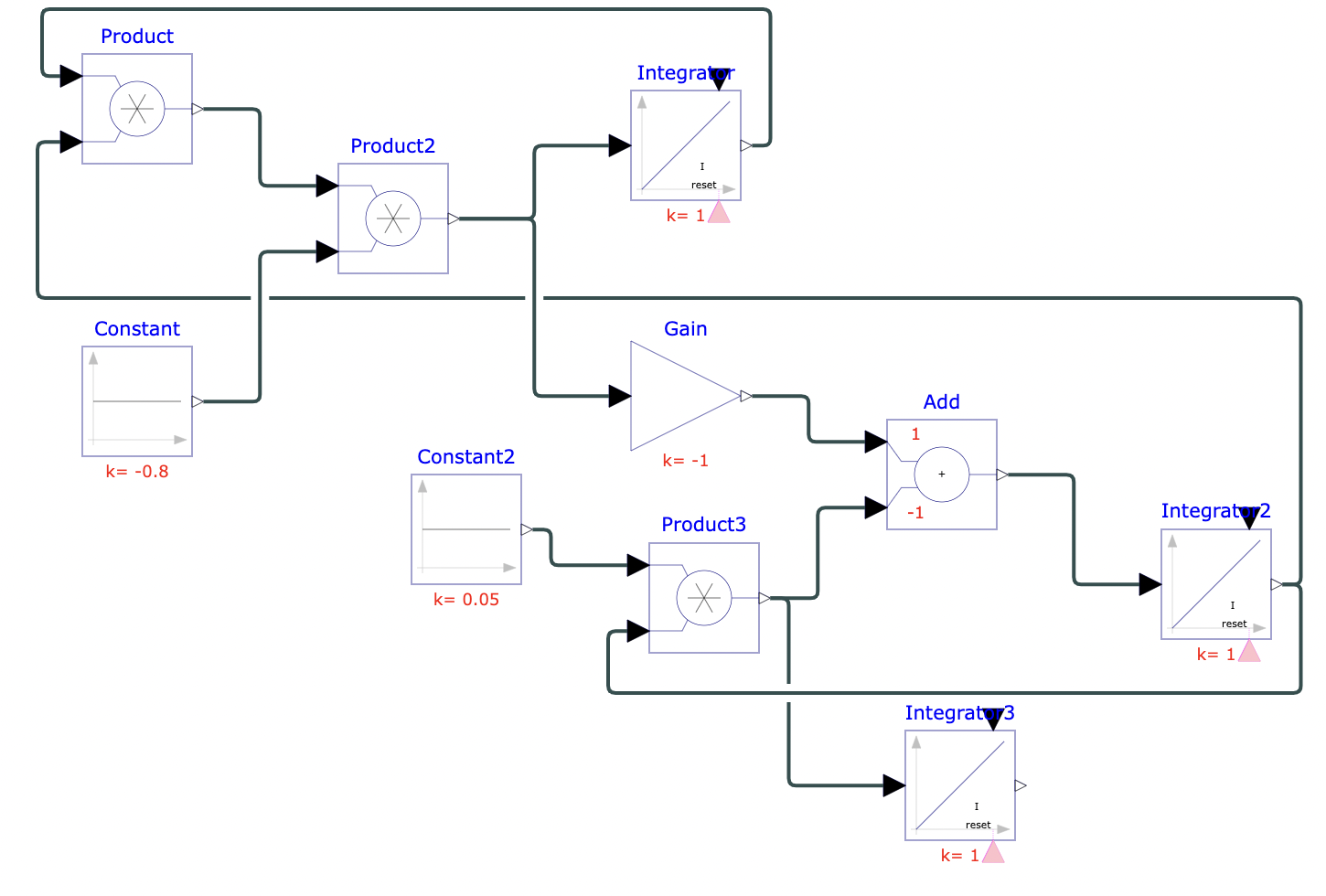
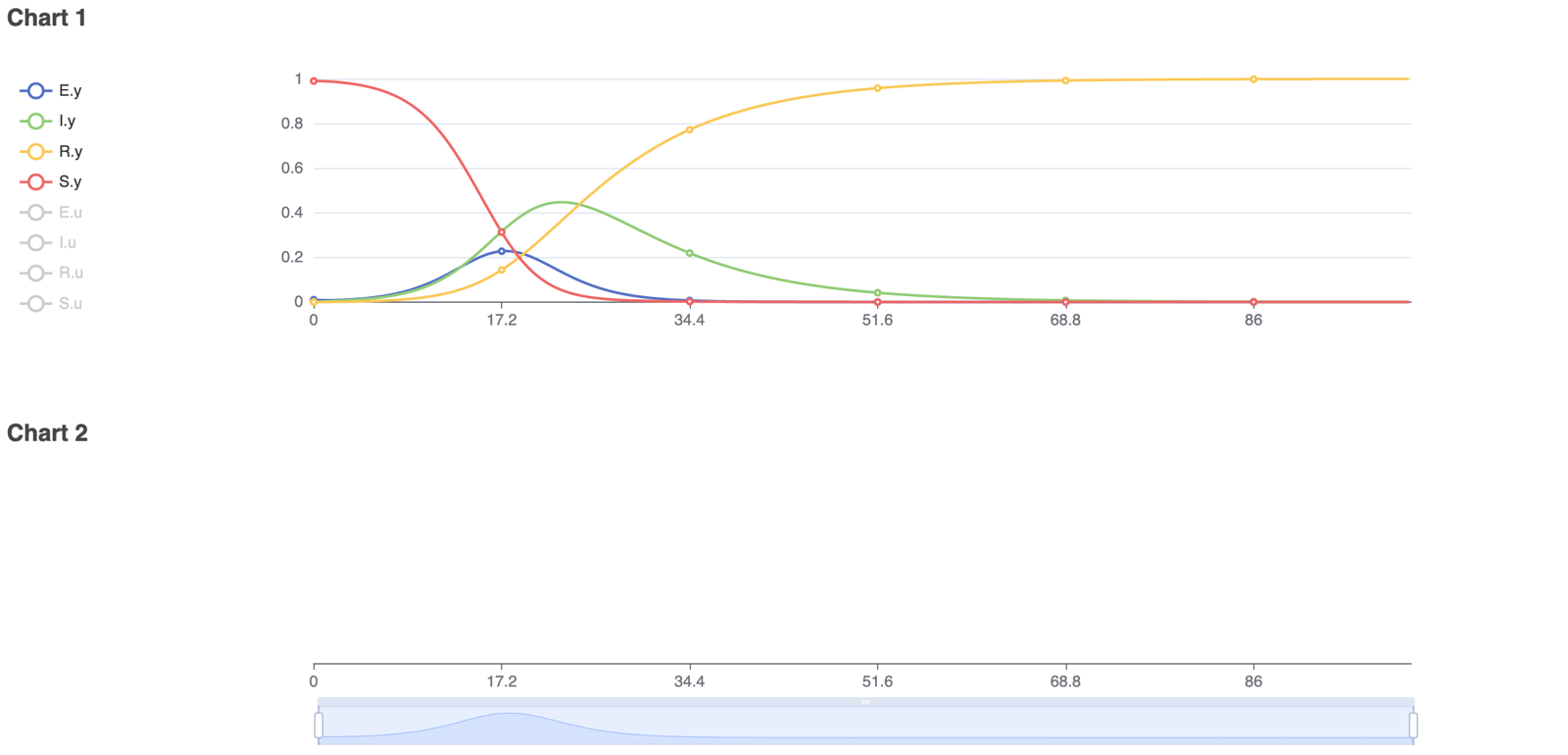
To model real-life diseases, ß, γ, and N can be changed to match the situation. For example, a highly infectious, non-fatal disease that appears in a closed population of 1, or 100%, has an infection rate of 0.8 and a recovery rate of 0.05. The resulting model predicts the behavior of the disease over a selected period. The figures below show the diagram created in Physhub and the corresponding charts ((Fig.1, Fig.2)).
Results
The model successfully simulates the changes in the number of susceptible, infected, and recovered individuals in a closed population over time. The simulation was run for 100 units of time. The number of susceptible individuals decreased following a logistic decay curve; the number of infectious individuals rapidly increased until time 15, then slowly decreased; and the number of recovered individuals increased following a logistic growth curve. As predicted in theory, all individuals became infectious and eventually recovered. In general, this model is able to accurately simulate infectious disease behavior and compartmental changes in a population given any set of realistic constants.