Modeling A Simple Pendulum
Theory
A simple pendulum consists of a mass suspended from a massless string fixed at a pivot point. When the mass is displaced to a certain angle and released, the pendulum will swing back and forth with periodic motion infinitely, assuming no outside forces. The motion of a simple pendulum can be obtained by analyzing the forces that act upon the mass at any given moment. The concept governing the motion of a pendulum is the idea that the total force applied to a moving body represents the motion of the body. For a linear system, this concept takes the form of the basic equation $F = ma$, where F is the total force, m is mass, and a is linear acceleration. In the case of a pendulum, the system involves rotational motion, so the force is instead torque, $\tau$.
Model
Equation
In a rotational system, the force (and motion) can be represented by $\tau = Ia$, where I is rotational inertia, and a is angular acceleration. Rotational inertia considers a mass rotating at a radius r from the axis of rotation and is represented by the equation $I = mr^{2}$. In a pendulum, r is the length of the string, l. Angular acceleration is the change in angular velocity over time, which is the change in angular rotation over time; this is represented by the second derivative of the angle, $\frac{d^{2}\theta}{dt^{2}}$. Together, the right side of the equation becomes $ml^{2}\frac{d^{2}\theta}{dt^{2}}$. The left side can be derived from a free body diagram^1 using trigonometry. The magnitude of torque is found to be $- mgl \bullet sin(\theta)$. Combining both sides of the equation results in $- mgl \bullet sin(\theta) = ml^{2}\frac{d^{2}\theta}{dt^{2}}$ , which can be simplified to $- g \bullet \sin\sin\ (\theta)\ = l\frac{d^{2}\theta}{dt^{2}}$. After rearranging the constants, the final equation is $\frac{d^{2}\theta}{dt^{2}} = - \sin\frac{g}{l}\sin\ (\theta)\ $.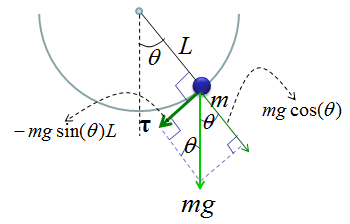
Parameters
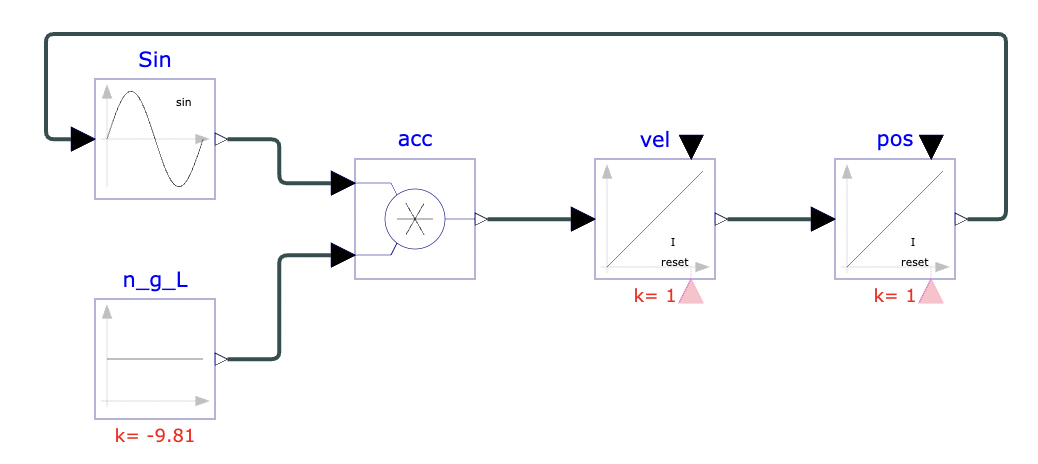
The parameters l, the length of the pendulum string, and g, gravitational force are constants. In the following Physhub model, the length is 1 meter. The initial displacement is $90{^\circ}$ or
$\frac{\pi}{2}$ radians, meaning the pendulum was pulled to a horizontal position before being released. The model starts with angular acceleration, the second derivative of $\theta$. Integrating both sides produces angular velocity. The y_start value of this Integrator block is 0, since the velocity at the chosen starting point is 0. Integrating one more time results in position, which is, in this case, the angle from the vertical position. The y_start of this Integrator is the initial displacement, $\frac{\pi}{2}$. The output of the position block is $\theta$, and this becomes the input of the sine function block. This model is simulated for 5 seconds.
Results
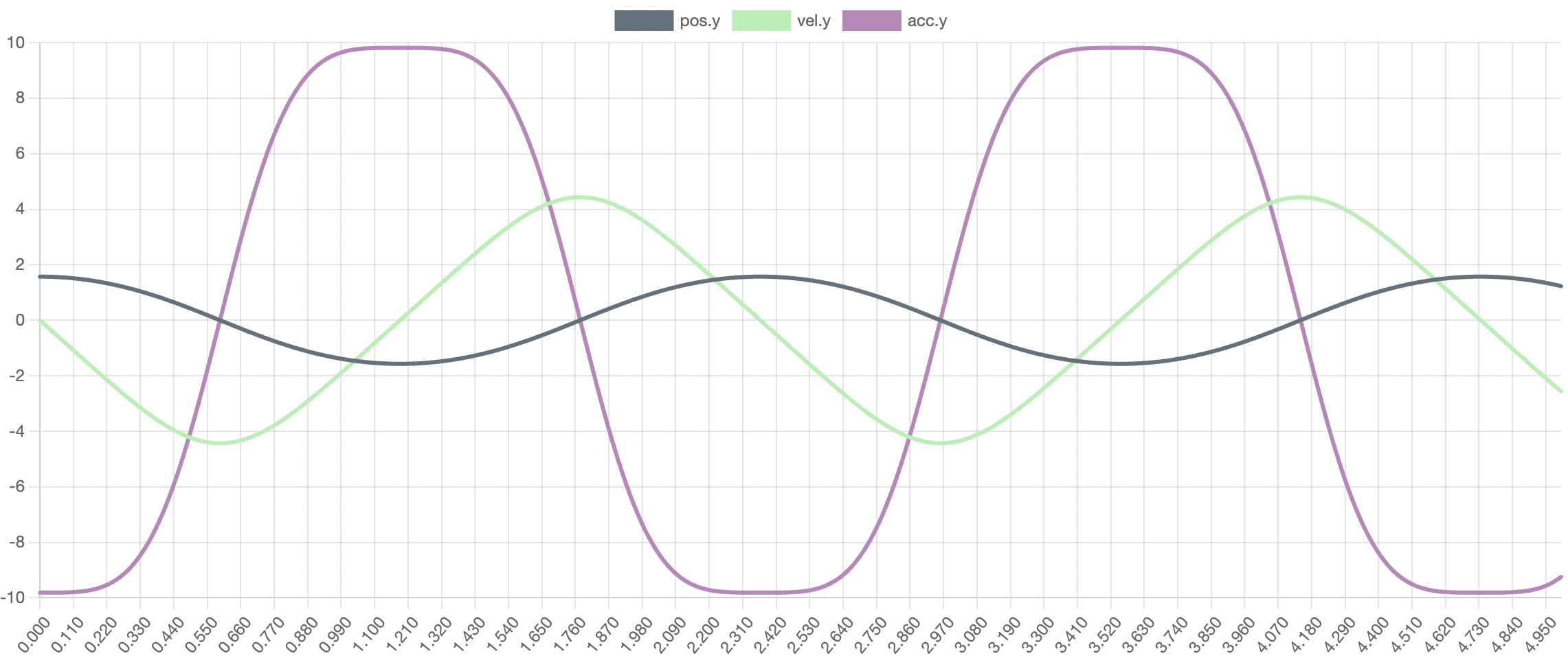
The model accurately shows the dynamics of motion of a simple pendulum with a 1-meter-long string starting at $90{^\circ}$ displacement. The model captures the periodic behavior of the acceleration, velocity, and angle of the pendulum.
Extension
The main limitation of this setup is that it cannot model a pendulum with a different initial displacement. However, the diagram can easily be modified to do so. The position Integrator should be replaced by a LimIntegrator block, and the outMax and y_start should be set to the initial displacement angle (in radians). For example, to model a
$45{^\circ}$ initial displacement, the above values should be set to $\frac{\pi}{4}$.